Stripy: A Python module for (constrained) triangulation in Cartesian coordinates and on a sphere.
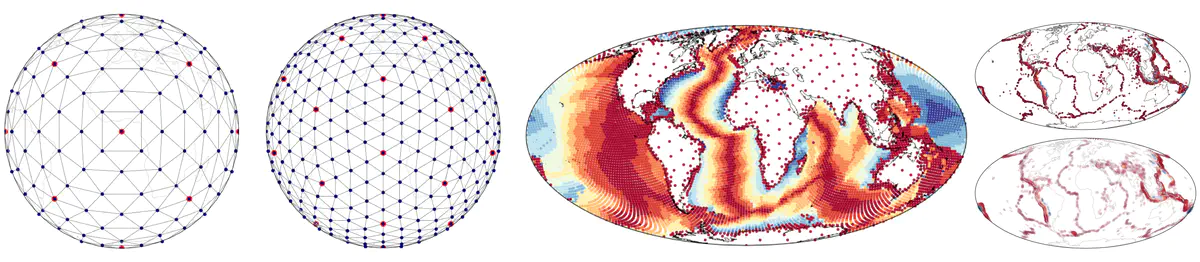 Samples meshes on the sphere produced by stripy.
Samples meshes on the sphere produced by stripy.Abstract
The triangulation of scattered points is a common problem in science and engineering when local neighbourhood information is required for computation. Typical applications include the calculation of neighbour relationships, interpolants, derivatives, and smoothly-fitting surfaces. A more specialised problem is the triangulation of points distributed on the surface of a sphere, nevertheless, this is important in most global geographical applications where data are registered in longitude and latitude and the Earth’s ellipticity can be considered as a second order effect.
Our package, stripy, is a python, numpy-based interface to the TRIPACK and STRIPACK Fortran code for (constrained) triangulation in Cartesian coordinates and on a sphere, respectively and includes routines from SRFPACK and SSRFPACK for interpolation (nearest neighbour, linear, and hermite cubic) and to evaluate derivatives. Our focus in developing an augmented set of wrappers for a venerable and widely used set of fortran subroutines has been on ease of use so that triangulated or scattered data on the sphere can be brought quickly into interactive jupyter notebooks for analysis and interrogation.
stripy is an object-oriented package that extends the functionality of the original collection of subroutine by adding a number of useful tools such as the construction of regular meshes on the sphere (icosahedral and octahedral each with face-centre-point variants, a triangulated cube and a truncated icosahedron with face-centre points that produces a C60 / soccerball mesh). stripy also includes functionality to refine meshes globally and locally by triangle or edge subdivision. We have taken some care to ensure that queries on the triangulations are vectorised within numpy queries. stripy offers a consistent API between the two coordinate system so users can transfer from Cartesian to spherical coordinates with minor changes to their code.
stripy includes the following functionality:
- Spherical and Cartesian triangulation of scattered points.
- Construction of Cartesian and Spherical meshes.
- Nearest-neighbour, linear, and hermite cubic interpolation.
- Evaluation of derivatives.
- Smoothing operations.
- Mesh refinement on line segments / triangle centroids.
- Fast point location with k-d tree interface with angular separation metric on the sphere.
Documentation
stripy is bundled with a linked collection of jupyter notebooks that can act as a user guide and an introduction to the package. The notebooks are split into matching sets for spherical and Cartesian triangulations. The notebooks cover:
- Introduction to the triangulation classes
- Use of the gridding tools
- Interpolation
- Gradient operations
- Smoothing operations
- Issues that arise with highly irregular data
- Refinement of triangulations
Particularly for the spherical notebooks, global geographical examples are appropriate and we use the familiar pattern of global coastlines when we plot the global distributions of vertices and edges.
We also provide some worked examples where we mix data that come with very different gridding strategies. The Crust 1.0 dataset is supplied as cell-centred values on a 1x1 degree grid of points (i.e. equally spaced in longitude and latitude) with no depth information, whereas the related litho 1.0 dataset is supplied as columns of depth-values at points that are distributed on a seven-times-refined icosahedral mesh. The mixing and matching of these datasets in global maps was the original use-case for stripy.
All documentation can be accessed from within the module via a python function that installs the notebooks at a filesystem location specified by the user at run time.
Installation, Dependencies and Usage
stripy requires numpy and a fortran compiler such as gfortran to compile the fortran90 versions of the (S)TRIPACK and (S)SRFPACK routines that are included with the distribution. The optional k-d tree methods on the meshes require the scipy.spatial module. The documentation is supplied in the form of jupyter notebooks (the jupyter system is a dependency) which also have optional dependencies for the cartopy mapping package and the lavavu embedded, 3D visualisation package. stripy and all python dependencies can be installed through the pypi.org pip package. However, the fortran compiler, and several of the dependencies for cartopy and lavavu may cause problems for inexperienced users. We therefore provided a fully build docker image and a deployment of the documentation / examples on mybinder.org
Acknowledgements
Louis Moresi would like to acknowledge the support of the CIDER 2016 summer program (NSF grant EAR-1135452) during which this project was conceived. Development of stripy was financially supported by AuScope (www.auscope.org.au) which is funded by the Australian Government through the National Collaborative Research Infrastructure Strategy.